复数与单位根
复数
虚数是数学中引入的一种数，用来表示不能直接表示的数。例如，$\sqrt{-1}$，我们无法直接表示，因此引入虚数$i$，使得$\sqrt{-1}=i$。
虚数满足以下性质：
1、$i^2=-1$
2、$i^3=-i$
3、$i^4=1$
4、$i^5=i$
5、$i^6=-1$
2、$i^3=-i$
3、$i^4=1$
4、$i^5=i$
5、$i^6=-1$
复数由两部分组成，实部和虚部，记作$a+bi$，其中$a$是实部，$b$是虚部。复数可以看作一个简单的多项式，所以加减乘除都和多项式一致。
单位根
首先介绍复平面。复平面由实数轴和虚数轴组成，实数轴是$x$轴，虚数轴是$y$轴。复数$a+bi$在复平面上的表示为复平面上的一个点，$a$是$x$轴上的坐标，$b$是$y$轴上的坐标。
复数在复平面上可以表示为一个向量，向量的长度是复数的模（长度），向量的角度是复数的辐角（向量与实轴的夹角）。
我们可以在复平面上画一个单位圆，也就是圆心是原点，半径是1的圆。
我们知道欧拉定理：
$$e^{i\theta}=\cos\theta+i\sin\theta$$
可以发现一个公式：$e^{\alpha i}e^{\beta i}=e^{(\alpha+\beta)i}$，因此，我们可以发现，这种形式的乘法，其实相当于进行了角度的旋转操作。不论如何，模长始终是一，因为不论角度如何变化，$sin^2+cos^2=1$。
单位根是复平面单位圆上的点，满足方程$z^n=1$。相当于是在复平面上把单位圆$n$等分，然后取这些点：
$$\omega_n^k=e^{\frac{2\pi}{n}ki}=\cos\frac{2\pi}{n}k+i\sin\frac{2\pi}{n}k$$
其中$k$是第$k$个点，$k\in[0,n)$。$\frac{2\pi}{n}$的含义是把单位圆$n$等分，相邻两个点之间的角度。
单位根的一些性质：
1、$\omega_{n}^{k}=\omega_{n}^{k+n}$
2、$\omega_{n}^{k}=\omega_{n}^{k\pmod n}$
3、$\omega_{n}^{k+n/2}=-\omega_{n}^{k}$
4、$\omega_{np}^{kp}=\omega_{n}^{k}$
2、$\omega_{n}^{k}=\omega_{n}^{k\pmod n}$
3、$\omega_{n}^{k+n/2}=-\omega_{n}^{k}$
4、$\omega_{np}^{kp}=\omega_{n}^{k}$
性质三可以从旋转的角度来思考，加$n/2$相当于转了半圈，因此实部和虚部都取反。
FFT
多项式
给定一个多项式$f(x)=\sum_{i=0}^{n-1}a_i x^i$。
这种形式也叫做多项式的系数表示法。
我们知道两点确定一条直线（一次函数），三点确定一个二次函数，$n$个点可以确定一个$n-1$次函数。因此，如果我们有$n$个点，就可以确定一个$n-1$次函数。
对于$f(x)$，我们可以带入$n$个不同的值，得到$n$个点，从而唯一的确定这个多项式。也就是把这个多项式表示为：
$$(x_0,f(x_0)),(x_1,f(x_1)),(x_2,f(x_2)),\cdots,(x_{n-1},f(x_{n-1}))$$
这种形式也叫做多项式的点值表示法。
点值表示法在计算多项式的运算的时候非常简便，例如，两个多项式$f,g$进行加法，对于点值表示法来说，只需要对应位置相加即可，也就是：
$$(x_0,f(x_0)+g(x_0)),(x_1,f(x_1)+g(x_1)),(x_2,f(x_2)+g(x_2)),\cdots,(x_{n-1},f(x_{n-1})+g(x_{n-1}))$$
同理，对于乘法，只需要对应位置相乘即可，也就是：
$$(x_0,f(x_0)g(x_0)),(x_1,f(x_1)g(x_1)),(x_2,f(x_2)g(x_2)),\cdots,(x_{n-1},f(x_{n-1})g(x_{n-1}))$$
我们想要带入一个具体的值$x_0$，计算多项式的值，我们可以拆分成两个向量的乘积：
$$f(x_0)=\sum_{i=0}^{n-1}a_i x_0^i\\=
\begin{bmatrix}
x_0^0 & x_0^1 & x_0^2 & \cdots & x_0^{n-1} \\
\end{bmatrix}\times \begin{bmatrix}
a_0 \\
a_1 \\
a_2 \\
\vdots \\
a_{n-1} \\
\end{bmatrix}$$
这样，如果我们需要多次带入值进行求解，就可以写作：
$$\begin{bmatrix}
x_0^0 & x_0^1 & x_0^2 & \cdots & x_0^{n-1} \\
x_1^0 & x_1^1 & x_1^2 & \cdots & x_1^{n-1} \\
x_2^0 & x_2^1 & x_2^2 & \cdots & x_2^{n-1} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
x_{m-1}^0 & x_{m-1}^1 & x_{m-1}^2 & \cdots & x_{m-1}^{n-1} \\
\end{bmatrix}\times \begin{bmatrix}
a_0 \\
a_1 \\
a_2 \\
\vdots \\
a_{n-1} \\
\end{bmatrix}=\begin{bmatrix}
f(x_0) \\
f(x_1) \\
f(x_2) \\
\vdots \\
f(x_{m-1}) \\
\end{bmatrix}$$
最左侧的矩阵也叫做Vandermonde matrix（范德蒙德矩阵）。范德蒙德矩阵的一个性质是当代入的这$m$个数字两两互异，其矩阵的秩为$min(n,m)$。当$n=m$时，其秩为$n$，因此是可逆的。
$FFT$解决多项式乘法，就是带入$n$个合适的不同的值，然后快速求值，将多项式的乘法变成点值表示法，从而进行快速的乘法计算，最后再将点值表示法还原成系数表示法。
多项式乘法其实就是所谓的一种卷积，其表现形式为：
$$f(x)=\sum_{i=0}^{n-1}a_i x^i,g(x)=\sum_{i=0}^{n-1}b_i x^i$$
$$f(x)g(x)=\sum_{i=0}^{n-1}\sum_{j=0}^{n-1}a_i b_j x^{i+j}\\=\sum_{k=1}^{n}\sum_{i+j=k}a_i b_j x^k$$
DFT
$DFT$是离散傅里叶变换，将多项式的系数表示法转化为点值表示法。
这里将$\omega_{n}^k$作为值带入，带入的值是复数，因此$f(\omega_{n}^k)=\sum_{i=0}^{n-1}a_i \omega_{n}^{ki}$。
为了保证算法的正确性，我们一般会把$n$扩大成$2$的幂，高位没有的部分补0。
$DFT$把一个多项式分成奇偶两部分，也就是：
$$
\begin{aligned}
f(x) & =a_0 x^0+a_1 x^1+a_2 x^2+\cdots+a_{n-1} x^{n-1}\\
& = (a_0+a_2 x^2+\cdots+a_{n-2} x^{n-2})+(a_1 x^1 +a_3 x^3+\cdots+a_{n-1} x^{n-1})\\
&= (a_0+a_2 x^2+\cdots+a_{n-2} x^{n-2})+x(a_1+a_3 x^2+\cdots+a_{n-1} x^{n-2})\\
&= f_0(x^2)+x f_1(x^2)
\end{aligned}
$$
我们将$\omega_{n}^{k}$带入，得到：
1、如果$k < \frac n2$
$$\begin{aligned}
f(\omega_{n}^{k}) & =f_0(\omega_{n}^{2k})+\omega_{n}^{k}f_1(\omega_{n}^{2k})\\
& =f_0(\omega_{n/2}^{k})+\omega_{n}^{k}f_1(\omega_{n/2}^{k})\\
\end{aligned}$$
2、如果$k \ge \frac n2$，我们可以把这个$k$表述为$k+\frac n2(k< \frac n2)$
$$\begin{aligned}
f(\omega_{n}^{k}) & =f_0(\omega_{n}^{2k+n})+\omega_{n}^{k+\frac n2}f_1(\omega_{n}^{2k+n})\\
& =f_0(\omega_{n}^{2k})+\omega_{n}^{k+\frac n2}f_1(\omega_{n}^{2k})\\
& =f_0(\omega_{n/2}^{k})+\omega_{n}^{k+\frac n2}f_1(\omega_{n/2}^{k})\\
& =f_0(\omega_{n/2}^{k})-\omega_{n}^{k}f_1(\omega_{n/2}^{k})\\
\end{aligned}$$
对比可以得知，两个式子只是中间一个正号一个负号的差别。
因此，只要我们能够知道$f_0,f_1$在$\omega_{n/2}{0},\omega_{n/2}^{1},\cdots,\omega_{n/2}^{n/2-1}$的 **值** ，就可以求出$f$在$\omega_{n}^{0},\omega_{n}^{1},\cdots,\omega_{n}^{n-1}$的值。
也就是，我们不按照之前的$f(\omega_{n}^{k})=\sum_{i=0}^{n-1}a_i \omega_{n}^{ki}$进行计算了，而是按照$f(\omega_{n}^{k})=f_0(\omega_{n/2}^{k})\pm \omega_{n}^{k}f_1(\omega_{n/2}^{k})$来进行计算，这样就可以把问题规模缩小一半。
可以发现，这时候进行求值的数量减半了。
由于$n$是$2$的幂，所以$f_0,f_1$也可以按照同样的方法拆分，直到拆分到长度为$1$，最后回溯计算即可。这就是DFT的分治过程。
这个递归分治过程的一个参考代码：
#include <cstdio>
#include <cmath>
#define Maxn 1350000
using namespace std;
const double Pi=acos(-1);
int n,m;
struct CP
{
CP (double xx=0,double yy=0){x=xx,y=yy;}
double x,y;
CP operator + (CP const &B) const
{return CP(x+B.x,y+B.y);}
CP operator - (CP const &B) const
{return CP(x-B.x,y-B.y);}
CP operator * (CP const &B) const
{return CP(x*B.x-y*B.y,x*B.y+y*B.x);}
//除法没用
}f[Maxn<<1],sav[Maxn<<1];
void dft(CP *f,int len)
{
if (len==1)return ;//边界
//指针的使用比较巧妙
CP *f0=f,*f1=f+len/2;
for (int k=0;k<len;k++)sav[k]=f[k];
for (int k=0;k<len/2;k++)//分奇偶打乱
{f0[k]=sav[k<<1];f1[k]=sav[k<<1|1];}
dft(f0,len/2);
dft(f1,len/2);//处理子问题
//由于每次使用的单位根次数不同(len次单位根),所以要重新求。
CP tG(cos(2*Pi/len),sin(2*Pi/len)),buf(1,0);
for (int k=0;k<len/2;k++){
//这里buf = (len次单位根的第k个)
sav[k]=f0[k]+buf*f1[k];//(1)
sav[k+len/2]=f0[k]-buf*f1[k];//(2)
buf=buf*tG;//得到下一个单位根。
}for (int k=0;k<len;k++)f[k]=sav[k];
}
int main()
{
scanf("%d",&n);
for (int i=0;i<n;i++)scanf("%lf",&f[i].x);
//一开始都是实数,虚部为0
for(m=1;m<n;m<<=1);
//把长度补到2的幂,不必担心高次项的系数,因为默认为0
dft(f,m);
for(int i=0;i<m;++i)
printf("(%.4f,%.4f)\n",f[i].x,f[i].y);
return 0;
}IDFT
$IDFT$是离散傅里叶逆变换，将点值表示法转化为系数表示法。
省流版：$IDFT$就是$DFT$的逆运算，因此只需要将$DFT$中的$\omega_{n}^{k}$换成$\omega_{n}^{-k}$，最后每一个系数再除以$n$即可。至于为什么这么做，我们在后续的单位根反演的知识点中会回过头来再看。
递归版FFT
实现的是洛谷P3803 【模板】多项式乘法（FFT）：
#include<bits/stdc++.h>
#define Maxn 2000005
#define ll long long
using namespace std;
const double Pi=acos(-1);
template<typename T>
void read(T &x) {x = 0;char ch = getchar();ll f = 1;while(!isdigit(ch)){if(ch == '-')f *= -1;ch = getchar();}while(isdigit(ch)){x = x * 10 + ch - 48; ch = getchar();}x *= f;}
template<typename T, typename... Args>
void read(T &first, Args& ... args) {read(first);read(args...);}
template<typename T>
void write(T arg) {T x = arg;if(x < 0) {putchar('-'); x =- x;}if(x > 9) {write(x / 10);}putchar(x % 10 + '0');}
template<typename T, typename ... Ts>
void write(T arg, Ts ... args) {write(arg);if(sizeof...(args) != 0) {putchar(' ');write(args ...);}}
int n,m;
struct CP{
CP (double xx=0,double yy=0){x=xx,y=yy;}
double x,y;
CP operator + (CP const &B) const{return CP(x+B.x,y+B.y);}
CP operator - (CP const &B) const{return CP(x-B.x,y-B.y);}
CP operator * (CP const &B) const{return CP(x*B.x-y*B.y,x*B.y+y*B.x);}
}f[Maxn<<1],g[Maxn<<1],sav[Maxn<<1];
int ans[Maxn<<1];
void fft(CP *f,int len,int type){
if (len==1)return ;
CP *f0=f,*f1=f+len/2;
for(int k=0;k<len;k++)sav[k]=f[k];
for(int k=0;k<len/2;k++){f0[k]=sav[k<<1];f1[k]=sav[k<<1|1];}
fft(f0,len/2,type);fft(f1,len/2,type);
CP tG(cos(2*Pi/len),type*sin(2*Pi/len)),buf(1,0);
for (int k=0;k<len/2;k++){
sav[k]=f0[k]+buf*f1[k];
sav[k+len/2]=f0[k]-buf*f1[k];
buf=buf*tG;
}for (int k=0;k<len;k++)f[k]=sav[k];
}
int main(){
read(n,m);
for(int i=0;i<=n;i++) scanf("%lf",&f[i].x);
for(int i=0;i<=m;i++) scanf("%lf",&g[i].x);
int lim=1;
for(;lim<=n+m;lim<<=1);
fft(f,lim,1);fft(g,lim,1);
for(int i=0;i<=lim;i++) f[i]=f[i]*g[i];
fft(f,lim,-1);
for(int i=0;i<=lim;i++) ans[i]+=(int)(f[i].x/lim+0.5);
for(int i=0;i<n+m+1;i++) write(ans[i]),putchar(' ');
return 0;
}非递归版FFT（蝴蝶变换）
递归版的$FFT$实际上比较慢，性能比较差，所以我们要改成非递归版。观察$FFT$的递归过程：
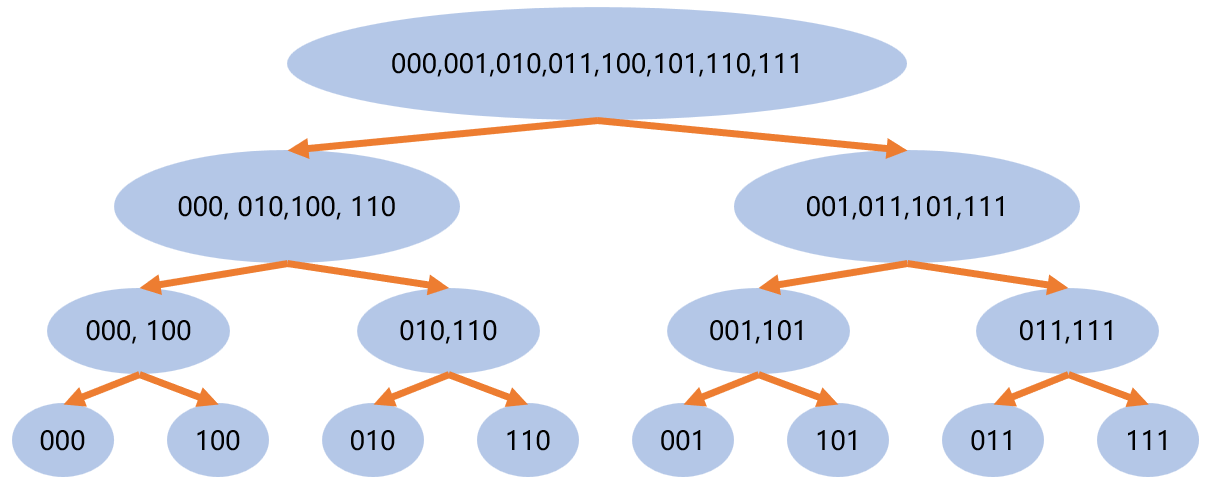
可以发现一个非常人类智慧的规律，原序列的每个下标，在递归的最后一层的位置，正好是其下标的二进制翻转过来。
所以我们可以提前把序列排列成最后一层的顺序，然后按照公式：
$$f(\omega_{n}^{k})=f_0(\omega_{n/2}^{k})\pm \omega_{n}^{k}f_1(\omega_{n/2}^{k})$$
直接向上计算，这样就避免了递归。
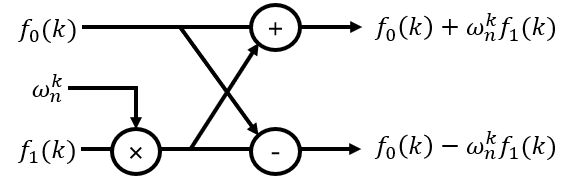
也正因这个图，我们也称这个运算叫做蝴蝶变换。
最终的$FFT$模板：
struct Complex{
double x,y;
Complex(double xx=0,double yy=0):x(xx),y(yy){}
}a[N],b[N];
Complex operator + (const Complex& c,const Complex& d){return Complex(c.x+d.x,c.y+d.y);}
Complex operator - (const Complex& c,const Complex& d){return Complex(c.x-d.x,c.y-d.y);}
Complex operator * (const Complex& c,const Complex& d){return Complex(c.x*d.x-c.y*d.y,c.x*d.y+c.y*d.x);}
void FFT(Complex * A,int type){
for(int i=0;i<limit;i++)//重新排列元素，变成最后一层顺序
if(i<r[i]) swap(A[i],A[r[i]]);
for(int mid=1;mid<limit;mid<<=1){//mid是当前区间长度
Complex Wn(cos(Pi/mid),type*sin(Pi/mid));//单位根初始化
for(int len=mid<<1,j=0;j<limit;j+=len){//扫描每块区间
Complex w(1,0);//最开始的单位根
for(int k=0;k<mid;k++,w=w*Wn){//计算区间内所有元素的值
Complex x=A[j+k],y=w*A[j+mid+k];
A[j+k]=x+y;
A[j+mid+k]=x-y;
}
}
}
}不过我们需要先在$\text{main}$函数中预处理$r$数组，也就是每个下标的翻转：
while(limit<=n+m) limit<<=1,L++;
for(int i=0;i<=limit;i++){
r[i]=(r[i>>1]>>1)|((i&1)<<(L-1));
}一个简单的递推过程，观察一下：
$r[i>>1]$相当于把$i$的最后一位去掉（翻转后的最高位去掉）。这样会导致高位补一个$0$，所以再右移一位，所以有了$r[i>>1]>>1$这一条。这样一来，我们利用之前已经得到的结果$r[i>>1]$，就完成了除了最高位的翻转。所以我们再把最高位补上，也就是或上$((i\&1)<<(L-1))$。
三步变两步优化
在计算多项式乘法的时候，我们需要先调用两次$FFT$，使得两个多项式变成系数表示法，然后进行点值相乘，最后再调用一次$FFT$，使得结果从点值表示法变回系数表示法。这样用到了三次$FFT$。
我们考虑到如下的公式：
$$(a+bi)^2=a^2-b^2+2abi$$
可以发现，虚部正好有乘法部分。所以我们可以把两个多项式放到实部和虚部，对自身求平方，这样就只需要两次$FFT$就可以了。
三步变两步优化版多项式乘法：
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=4e6+5;
const double Pi=acos(-1);
struct Complex{
double x,y;
Complex(double xx=0,double yy=0):x(xx),y(yy){}
}a[N];
int n,m,r[N];
Complex operator + (const Complex& c,const Complex& d){return Complex(c.x+d.x,c.y+d.y);}
Complex operator - (const Complex& c,const Complex& d){return Complex(c.x-d.x,c.y-d.y);}
Complex operator * (const Complex& c,const Complex& d){return Complex(c.x*d.x-c.y*d.y,c.x*d.y+c.y*d.x);}
void FFT(Complex * A,int limit,int type){
for(int i=0;i<limit;i++){
if(i<r[i]) swap(A[i],A[r[i]]);
}
for(int mid=1;mid<limit;mid<<=1){
Complex Wn(cos(Pi/mid),type*sin(Pi/mid));
for(int R=mid<<1,j=0;j<limit;j+=R){
Complex w(1,0);
for(int k=0;k<mid;k++,w=w*Wn){
Complex x=A[j+k],y=w*A[j+mid+k];
A[j+k]=x+y;
A[j+mid+k]=x-y;
}
}
}
if(type==-1){
for(int i=0;i<limit;i++){
A[i].x/=limit;
A[i].y/=limit;
}
}
}
int main(){
scanf("%d%d",&n,&m);
for(int i=0;i<=n;i++) scanf("%lf",&a[i].x);
for(int i=0;i<=m;i++) scanf("%lf",&a[i].y);
int limit=1,L=0;
while(limit<=n+m) limit<<=1,L++;
for(int i=1;i<limit;i++) r[i]=(r[i>>1]>>1)|((i&1)<<L-1);
FFT(a,limit,1);
for(int i=0;i<=limit;i++) a[i]=a[i]*a[i];
FFT(a,limit,-1);
for(int i=0;i<=n+m;i++){
printf("%d ",int(a[i].y/2+0.5));
}
return 0;
}习题：
P8958 「CGOI-3」残暴圣所
很显然，这个题是一个括号序列相关问题，所以我们可以使用卡特兰数。在此，卡特兰数的含义为：给定 $n$ 个左括号和 $n$ 个右括号，求合法的括号序列个数。
我们利用卡特兰数的递推公式就可以求出卡特兰数：
$$C_n=\dfrac{4n-2}{n+1}C_{n-1}$$
对于本题来说，我们考虑枚举括号，然后考虑括号对答案产生的贡献。可以想到，对于一对括号$i,j$来说，内部的合法的括号序列的数量为$C_{\frac{j-i-1}{2}}$，外部的为$C_{\frac{2n+i-j-1}{2}}$，所以答案就是：
$$\sum_{i=1}^{2n}\sum_{j=i+1}^{2n}C_{\frac{j-i-1}{2}}C_{\frac{2n+i-j-1}{2}}a_i a_j [2\not| j-i]$$
显然这样直接去枚举时间复杂度是$O(n^2)$的，考虑推一下式子：
$$
\begin{aligned}
&\sum_{i=1}^{2n}\sum_{j=i+1}^{2n}C_{\frac{j-i-1}{2}}C_{\frac{2n+i-j-1}{2}}a_i a_j [2\not| j-i]\\
(t=j-i)&=\sum_{2\not| t}^{2n}\sum_{i=1}^{2n-t}C_{\frac{t-1}{2}}C_{\frac{2n-t-1}{2}}a_{i}a_{i+t}\\
&=\sum_{2\not| t}^{2n}C_{\frac{t-1}{2}}C_{\frac{2n-t-1}{2}}\sum_{i=1}^{2n-t}a_{i}a_{i+t}\\
\end{aligned}
$$
可以发现前面卡特兰数的部分我们可以线性求解，问题是后面的求和部分：
$$\sum_{i=1}^{2n-t}a_i a_{i+t}$$
我们可以尝试把这个式子的形式往卷积的形式上靠，设$A_i=a_i,B_i=a_{2n-i}$，那么原式就是：
$$\sum_{i=1}^{2n-t}A_iB_{2n-t-i}$$
我们换个形式：
$$\sum_{i+j=2n-t}A_iB_j$$
可以发现这正好是一个卷积的形式，也就是说，这个式子其实是$[x^{2n-t}](A*B)(x)$，所以我们使用NTT求解即可。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
template<typename T>
void read(T &x) {x = 0;char ch = getchar();ll f = 1;while(!isdigit(ch)){if(ch == '-')f *= -1;ch = getchar();}while(isdigit(ch)){x = x * 10 + ch - 48; ch = getchar();}x *= f;}
template<typename T, typename... Args>
void read(T &first, Args& ... args) {read(first);read(args...);}
template<typename T>
void write(T arg) {T x = arg;if(x < 0) {putchar('-'); x =- x;}if(x > 9) {write(x / 10);}putchar(x % 10 + '0');}
template<typename T, typename ... Ts>
void write(T arg, Ts ... args) {write(arg);if(sizeof...(args) != 0) {putchar(' ');write(args ...);}}
const int N=4e6+5,mod=998244353,g=3,gi=332748118;
int n;
ll a[N],b[N],r[N],inv[N],catlan[N];
ll qpow(ll a,ll b){
ll ans=1;
while(b){
if(b&1) ans=ans*a%mod;
a=a*a%mod;
b>>=1;
}
return ans;
}
void NTT(ll * A,int limit,int type){
for(int i=0;i<limit;i++){
if(i<r[i]) swap(A[i],A[r[i]]);
}
for(int mid=1;mid<limit;mid<<=1){
//g原根，gi原根逆元
ll Wn=qpow(type==1?g:gi,(mod-1)/(mid<<1));
for(int j=0;j<limit;j+=(mid<<1)){
ll w=1;
for(int k=0;k<mid;k++,w=(w*Wn)%mod){
int x=A[j+k],y=w*A[j+k+mid]%mod;
A[j+k]=(x+y)%mod;
A[j+k+mid]=(x-y+mod)%mod;
}
}
}
}
void init(){
inv[0]=inv[1]=1;
for(int i=2;i<=n;i++) inv[i]=(mod-mod/i)*inv[mod%i]%mod;
catlan[0]=catlan[1]=1;
for(int i=2;i<=n;i++) catlan[i]=catlan[i-1]*(4*i-2)%mod*inv[i+1]%mod;
}
int main(){
read(n);n<<=1;init();
for(int i=1;i<=n;i++) read(a[i]),b[n-i]=a[i];
int limit=1,L=0;
while(limit<=(n<<1)) limit<<=1,L++;
for(int i=1;i<=limit;i++) r[i]=(r[i>>1]>>1)|((i&1)<<L-1);
NTT(a,limit,1),NTT(b,limit,1);
for(int i=0;i<=limit;i++) a[i]=a[i]*b[i]%mod;
NTT(a,limit,-1);
ll iv=qpow(limit,mod-2);
for(int i=0;i<=limit;i++) a[i]=a[i]*iv%mod;
ll ans=0;
for(int t=1;t<=n;t+=2){
ans+=catlan[t-1>>1]*catlan[n-t-1>>1]%mod*a[n-t]%mod;
ans%=mod;
}
write(ans);
return 0;
}P3723 [AH2017/HNOI2017] 礼物
很简单的推式子。假设我们要加的数字是$x$，那么差异值就是：
$$\sum_{i=1}^n (a_i-b_i+x)^2$$
简单拆一拆：
$$\sum_{i=1}^n a_i^2+\sum_{i=1}^n b_i^2+2x\sum_{i=1}^n(a_i-b_i)+nx^2-2\sum_{i=1}^n a_i b_i$$
可以发现除了最后一项以外，其他项都是定值。其中$nx^2+2x\sum_{i=1}^n(a_i -b_i)$是个二次函数，开头向上，求最小值的话，直接求导然后求导函数的根：
$$x=-\frac{\sum_{i=1}^n(a_i-b_i)}{n}$$
实际写代码的时候，注意向上取整和向下取整的问题，可以在根的附近求最小值。
剩下的，就是要求$2\sum_{i=1}^n a_i b_i$的最大值了。按照套路把式子变成：
$$\sum_{i=1}^n a_i b_{n-i}$$
显然是一个卷积形式。不过我们要求最大值的话，可以把$a$破环成链，后面复制一遍，然后卷积完从$n+1$到$2n$取最大值即可。
每一项的系数不会太大，所以可以使用FFT，也可以使用NTT
#include<bits/stdc++.h>
#define ll long long
using namespace std;
template<typename T>
void read(T &x) {x = 0;char ch = getchar();ll f = 1;while(!isdigit(ch)){if(ch == '-')f *= -1;ch = getchar();}while(isdigit(ch)){x = x * 10 + ch - 48; ch = getchar();}x *= f;}
template<typename T, typename... Args>
void read(T &first, Args& ... args) {read(first);read(args...);}
template<typename T>
void write(T arg) {T x = arg;if(x < 0) {putchar('-'); x =- x;}if(x > 9) {write(x / 10);}putchar(x % 10 + '0');}
template<typename T, typename ... Ts>
void write(T arg, Ts ... args) {write(arg);if(sizeof...(args) != 0) {putchar(' ');write(args ...);}}
const int N=4e5+5,mod=998244353,g=3,gi=332748118;
int n,m;
ll a[N],b[N],r[N];
ll qpow(ll a,ll b){
ll ans=1;
while(b){
if(b&1) ans=ans*a%mod;
a=a*a%mod;
b>>=1;
}
return ans;
}
void NTT(ll * A,int limit,int type){
for(int i=0;i<limit;i++){
if(i<r[i]) swap(A[i],A[r[i]]);
}
for(int mid=1;mid<limit;mid<<=1){
//g原根，gi原根逆元
ll Wn=qpow(type==1?g:gi,(mod-1)/(mid<<1));
for(int j=0;j<limit;j+=(mid<<1)){
ll w=1;
for(int k=0;k<mid;k++,w=(w*Wn)%mod){
int x=A[j+k],y=w*A[j+k+mid]%mod;
A[j+k]=(x+y)%mod;
A[j+k+mid]=(x-y+mod)%mod;
}
}
}
}
ll f(ll x,ll y){
return n*x*x+x*y;
}
int main(){
read(n,m);
ll ans=0,tmp=0;
for(int i=1;i<=n;i++){
read(a[i]);
a[i+n]=a[i],ans+=a[i]*a[i];
tmp+=a[i];
}
for(int i=1;i<=n;i++){
read(b[i]);
ans+=b[i]*b[i];
tmp-=b[i];
}
ll xmin=-tmp/n;
ans+=min(f(xmin,tmp<<1),min(f(xmin+1,tmp<<1),f(xmin-1,tmp<<1)));
reverse(b+1,b+1+n);
int limit=1,L=0;
while(limit<=(n*3)) limit<<=1,L++;
for(int i=1;i<=limit;i++) r[i]=(r[i>>1]>>1)|((i&1)<<L-1);
NTT(a,limit,1),NTT(b,limit,1);
for(int i=0;i<=limit;i++) a[i]=a[i]*b[i]%mod;
NTT(a,limit,-1);
ll iv=qpow(limit,mod-2);
for(int i=0;i<=limit;i++) a[i]=a[i]*iv%mod;
ll maxn=0;
for(int i=n+1;i<=2*n;i++){
maxn=max(maxn,a[i]);
}
ans-=(maxn<<1);
write(ans);
return 0;
}P3338 [ZJOI2014] 力
给出题目的定义：
$$F_j=\sum_{i=1}^{j-1}\frac{q_i q_j}{(i-j)^2}-\sum_{i=j+1}^{n}\frac{q_i q_j}{(i-j)^2}\\ E_j=\frac{F_j}{q_j}$$
显然：
$$E_j=\sum_{i=1}^{j-1}\frac{q_i}{(i-j)^2}-\sum_{i=j+1}^{n}\frac{q_i}{(i-j)^2}$$
也就是说，这就是我们想要的结果。那么我们尝试往卷积的形式上靠。
首先，设序列$q$的生成函数为$Q$，设函数$G(x)=\frac{1}{x^2}$，那么：
$$E_j=\sum_{i=1}^{j-1}Q(i)G(j-i)-\sum_{i=j+1}^{n}Q(i)G(i-j)$$
我们设$G(0)=0$，那么把第$j$项算进去也无伤大雅，也就是说：
$$E_j=\sum_{i=1}^{j}Q(i)G(j-i)-\sum_{i=j}^{n}Q(i)G(i-j)$$
显然，左侧已经是卷积形式了：
$$\sum_{i=1}^j Q(i)G(j-i)=\sum_{x+y=j}Q(x)G(y)=[x^j](Q*G)(x)$$
所以左侧很容易解决，关键是右侧式子的处理。我们观察一下式子：
$$\sum_{i=j}^n Q(i)G(i-j)$$
假设$A(i)=q_{n-i}$，显然也是之前说过的翻转的技巧。
$i$从$j$开始不太方便，我们改一下形式：
$$\begin{aligned}
\sum_{i=j+1}^n Q(i)G(i-j)&=\sum_{i=1}^{n-j} Q(i+j)G(i)\\
&=\sum_{i=1}^{n-j} A(n-(i+j))G(i)\\
(t=n-j)&=\sum_{i=1}^t A(t-i)G(i)\\
&=\sum_{x+y=t}A(x)G(y)\\&=[x^t](A*G)(x)
\end{aligned}
$$
那么这部分也变成了卷积的形式，我们使用FFT就可以快速解决了。也就是说，我们得到结论：
$$E_j=[x^j](Q*G)(x)-[x^{n-j}](A*G)(x)$$
本题精度损失有点严重，不要使用三步变两步优化。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=4e5+5;
const double Pi=acos(-1);
struct Complex{
double x,y;
Complex(double xx=0,double yy=0):x(xx),y(yy){}
}a[N],b[N],C[N];
Complex operator + (const Complex& c,const Complex& d){return Complex(c.x+d.x,c.y+d.y);}
Complex operator - (const Complex& c,const Complex& d){return Complex(c.x-d.x,c.y-d.y);}
Complex operator * (const Complex& c,const Complex& d){return Complex(c.x*d.x-c.y*d.y,c.x*d.y+c.y*d.x);}
int n,r[N];
double Q[N],A[N],G[N];
void FFT(Complex * A,int limit,int type){
for(int i=0;i<limit;i++){
if(i<r[i]) swap(A[i],A[r[i]]);
}
for(int mid=1;mid<limit;mid<<=1){
Complex Wn(cos(Pi/mid),type*sin(Pi/mid));
for(int R=mid<<1,j=0;j<limit;j+=R){
Complex w(1,0);
for(int k=0;k<mid;k++,w=w*Wn){
Complex x=A[j+k],y=w*A[j+mid+k];
A[j+k]=x+y;
A[j+mid+k]=x-y;
}
}
}
}
void convert(Complex*a,double*b,double*c,int limit){
for(int i=0;i<limit;i++){
a[i].x=b[i];a[i].y=0;
C[i].x=c[i];C[i].y=0;
}
FFT(a,limit,1);FFT(C,limit,1);
for(int i=0;i<=limit;i++) a[i]=a[i]*C[i];
FFT(a,limit,-1);
for(int i=0;i<=limit;i++) a[i].x=(a[i].x/limit+0.5);
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%lf",&Q[i]);
for(int i=0;i<n;i++) A[i]=Q[n-i];
for(int i=1;i<=n;i++) G[i]=1.0/i/i;
int limit=1,L=0;
while(limit<=(n<<1)) limit<<=1,L++;
for(int i=1;i<=limit;i++) r[i]=(r[i>>1]>>1)|((i&1)<<L-1);
convert(a,Q,G,limit);convert(b,A,G,limit);
for(int i=1;i<=n;i++){
printf("%lf\n",a[i].x-b[n-i].x);
}
return 0;
}
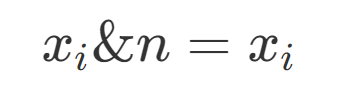
发表评论