群论是研究代数结构的一种数学分支,主要研究集合和运算之间的关系。群论的基本概念包括群、子群、同态、同构等。学会群论可以帮助我们更好地理解数学中的运算代数结构和很多问题内在的规律,提高抽象能力。
群由一个集合以及一个运算组成,比如$(Z,+)$就是一个群,其中$Z$是整数集合,$+$是加法运算。
首先,群的集合都要满足封闭性,即对于集合中的任意两个元素,它们的运算结果也必须在集合中。比如$(Z,+)$中,任意两个整数相加的结果仍然是整数。
**封闭性**:对于群$(S,*)$(这里的$*$不是乘法运算,而是代指某种运算,之后同理,除非标明是乘法,否则都代指某种运算),都有:
$$\forall a,b\in S,a*b\in S$$
幺半群
对于代数结构$(S,*)$,如果满足封闭性,并且有结合律,也就是:
$$\forall a,b,c\in S,(a*b)*c=a*(b*c)$$
那么$(S,*)$就是一个半群。
- 代数结构$(S,*)$满足封闭性,并且有结合律,那么$(S,*)$ 就是一个 **半群** 。
如果$(S,*)$是一个半群,并且存在幺元(也叫单位元),也就是:
$$\exists e\in S,\forall a\in S,e*a=a*e=a$$
那么$(S,*)$就是一个幺半群。
- 代数结构$(S,)$满足封闭性,并且有结合律,并且存在幺元,那么$(S,)$就是一个幺半群。
有的时候也会把单位元单独标出来,比如$(S,*,e)$,这里的$e$就是幺元。
如果代数结构$(S,*)$是幺半群,并且满足:
$$\forall a,b\in S,a*b=b*a$$
也就是有交换律,那么$(S,*)$就是一个交换幺半群。
举例,比如$(N,+),(Z,+),(Q,+),(R,+),(C,+)$(都是加法)都是交换幺半群,单位元是$0$。$(N,\times ),(Z,\times),(Q,\times),(R,\times),(C,\times)$(都是乘法)都是交换幺半群,单位元是$1$。
有没有不满足交换律的幺半群呢?有,比如在线性代数中,我们知道一个$n\times n$的矩阵的乘法并不满足交换律,但是矩阵乘法是满足结合律的,并且也有幺元(单位矩阵$I$),所以矩阵乘法构成一个幺半群。
练习:幺半群中的单位元是唯一的吗?请尝试证明。
证明:
假设有两个单位元$e_1,e_2\in S$,那么:
$$e_1*e_2=e_2*e_1=e_2$$
$$e_1*e_2=e_1$$
所以$e_1=e_2$,单位元是唯一的。
群
如果代数结构$(S,*)$是幺半群,并且满足:
$$\forall a\in S,a*a^{-1}=e$$
那么$(S,*)$就是一个群。注意,$a^{-1}$代指$a$的逆元,并不是$a$的倒数。
- 代数结构$(S,)$满足封闭性,并且有结合律,并且存在幺元,并且每个元素都有逆元,那么$(S,)$就是一个群。
注意,逆元是相互的,也就是说,$a$和$a^{-1}$互为逆元。
如果代数结构$(S,*)$是群,并且满足:
$$\forall a,b\in S,a*b=b*a$$
也就是有交换律,那么$(S,*)$就是一个交换群,也叫阿贝尔群。
两个群的例子
正方形的旋转群
我们把一个正方形的各种角度的旋转(都是向右旋转)都放到同一个集合内,记作$S$,$\Delta$表示做一次正方形的操作,那么$(S,\Delta)$就构成了一个群。
验证一下,首先是封闭性,封闭性显然。
然后是结合律,设$a,b,c\in S$,也就是说$a,b,c$都是正方形的操作,那么$a\Delta b\Delta c=a\Delta(b\Delta c)$,结合律成立。举个例子,旋转20度、旋转30度,旋转40度,以及旋转20度、(旋转30度,旋转40度)是等价的(先做旋转30度、旋转40度,再旋转20度)。
然后是幺元,旋转$0$度(可以认为是什么也不做)就是幺元。然后是逆元,旋转$20$度,逆元就是旋转$340$度。
最后是交换律,显然成立。
所以$(S,\Delta)$就是一个群,而且还是阿贝尔群。
但是如果集合中加入翻转(上下翻转和左右翻转),可以发现,依旧是一个群,但是不构成阿贝尔群了(翻转和旋转并不满足交换律)。
魔方的旋转群
魔方的转动操作也构成一个群的结构,只不过这个群不是阿贝尔群,因为魔方的旋转操作并不满足交换律。
子群
如果代数结构$(S,*)$是群,那么它的子集$(T,*)$也是群,那么$(T,*)$就叫做$(S,*)$的**子群**。也就是说,子群是群的一个子集,并且子集内的运算也满足群的性质。
阶
群$(S,*)$的阶,也就是群$(S,*)$的元素个数,记作$|S|$。
环与域
环的代数结构中存在两种运算,我们称之为加法和乘法,如果代数结构$(S,+,\times)$满足:
- $(S,+)$是一个交换群;
- $(S,\times)$是一个半群;
- $(S,+,\times)$满足分配律,也就是:
$$
\forall a,b,c\in S,a\times(b+c)=a\times b+a\times c
$$
$$
\forall a,b,c\in S,(a+b)\times c=a\times c+b\times c
$$
那么$(S,+,\times)$就是一个环。
- 代数结构$(S,+,\times)$满足$(S,+)$是一个交换群,$(S,\times)$是一个半群,并且$(S,+,\times)$满足分配律,那么$(S,+,\times)$就是一个环。
注意,对于结构$(S,\times )$如果只是半群而不是幺半群,那么我们也会称之为“无幺环”。
如果一个代数结构$(S,+,\times )$,满足:
- $(S,+)$是交换群
- $(S/\{0\},\times )$是交换群
- $(S,+,\times )$满足分配律
那么$(S,+,\times )$就是一个域。
- 代数结构$(S,+,\times )$满足$(S,+)$是交换群,$(S/{0},\times )$是交换群,并且$(S,+,\times )$满足分配律,那么$(S,+,\times )$就是一个域。
群、环、域与模运算
我们知道,假设模数为$m$,那么参与运算的元素集合为$S={x|0\leq x < m \wedge x\in Z}$。
那么,加法运算在这个几何上构成的代数结构$(S,+)$显然是一个阿贝尔群,因为:
- 封闭性:显然,因为$m$是整数,所以$S$中的任意两个元素相加的结果仍然在$S$中。
- 结合律:显然,因为整数加法满足结合律。
- 幺元:$0$是幺元,因为$0+x=x$。
- 逆元:对于任意$x\in S$,$m-x$是$x$的逆元,因为$x+(m-x)=0$。
- 交换律:显然,因为整数加法满足交换律。
所以$(S,+)$是一个阿贝尔群。
那么乘法运算呢?乘法运算在这个几何上构成的代数结构$(S/\{0\},\times )$并不一定构成阿贝尔群,因为并不是所有情况下,所有的数字都存在逆元。所以,我们知道$(s/\{0\},\times )$是一个幺半群。
所以在模意义下的代数结构$(S,+,\times )$是一个环,称为整数模$m$环,记作$\mathbb{Z}/m\mathbb{Z}$或者$\mathbb{Z}_m$。
结论:整数环$\mathbb{Z_m}$是一个域,当且仅当$m$是质数。
证明:当$m$是质数时,对于任意$a\in \mathbb{Z_m}$,$a$都有逆元,因为$a$与$m$互质,所以存在$b\in \mathbb{Z_m}$,使得$ab\equiv 1\pmod{m}$,所以$a$有逆元。
置换与置换环
置换:对于集合$S$,$S$的置换就是$S$到$S$的映射$f:S\to S$,可以理解为,对原本的元素进行重新排列。我们表示置换,通常用的形式为:
$$
\begin{pmatrix}
1 & 2 & 3 & 4 \\
2 & 1 & 4 & 3
\end{pmatrix}
$$
表示将$1$置换为$2$,将$2$置换为$1$,将$3$置换为$4$,将$4$置换为$3$。
例如,我们把${1,2,3}$的$3!=6$个置换看作函数时如下所示:
$$
\begin{pmatrix}
1 & 2 & 3 \\
1 & 2 & 3 \\
\end{pmatrix}
$$
$$
\begin{pmatrix}
1 & 2 & 3 \\
1 & 3 & 2 \\
\end{pmatrix}
$$
$$
\begin{pmatrix}
1 & 2 & 3 \\
2 & 1 & 3 \\
\end{pmatrix}
$$
$$
\begin{pmatrix}
1 & 2 & 3 \\
2 & 3 & 1 \\
\end{pmatrix}
$$
$$
\begin{pmatrix}
1 & 2 & 3 \\
3 & 1 & 2 \\
\end{pmatrix}
$$
$$
\begin{pmatrix}
1 & 2 & 3 \\
3 & 2 & 1 \\
\end{pmatrix}
$$
我们把这个集合记作$S_3$。既然置换是函数,那么就可以进行合成。假设
$$
f=\begin{pmatrix}
1 & 2 & \cdots & n \\
i_1 & i_2 & \cdots & i_n \\
\end{pmatrix}
$$
$$
g=\begin{pmatrix}
1 & 2 & \cdots & n \\
j_1 & j_2 & \cdots & j_n \\
\end{pmatrix}
$$
是$\{1,2,\cdots,n\}$的置换,那么$g\circ f$就是:
$$
g\circ f=\begin{pmatrix}
1 & 2 & \cdots & n \\
j_1 & j_2 & \cdots & j_n \\
\end{pmatrix}\circ \begin{pmatrix}
1 & 2 & \cdots & n \\
i_1 & i_2 & \cdots & i_n \\
\end{pmatrix}= \begin{pmatrix}
1 & 2 & \cdots & n \\
j_{i_1} & j_{i_2} & \cdots & j_{i_n} \\
\end{pmatrix}
$$
也就是说,先进行$f$置换,再进行$g$置换。也可以表示为$(g\circ f)(k)=g(f(k))=j_{i_k}$。
置换的合成满足结合律,有封闭性,并且存在幺元(恒等置换,也就是每个值都向自己映射),并且每个置换都有逆元(逆置换),所以$(S_n,\circ )$就是一个群,叫做**置换群**。
除了上面的两行表示置换,我们可以使用一行表示置换,比如:
$$
\begin{pmatrix}
1 & 2 & 3 & 4 \\
2 & 1 & 4 & 3
\end{pmatrix}
$$
可以表示为:
$$
(1,2)(3,4)
$$
表示将$1$置换为$2$,将$2$置换为$1$,将$3$置换为$4$,将$4$置换为$3$。
再举个例子,例如:
$$
\begin{pmatrix}
1 & 2 & 3 & 4 & 5 & 6 & 7\\
4 & 1 & 7 & 6 & 3 & 2 & 5
\end{pmatrix}
$$
可以表示为:
$$
(1,4,6,2)(3,7,5)
$$
这种形式的置换叫做循环置换。可以发现,上面这个例子的置换成了两个小循环,一个循环是$1,4,6,2$,另一个循环是$3,7,5$。
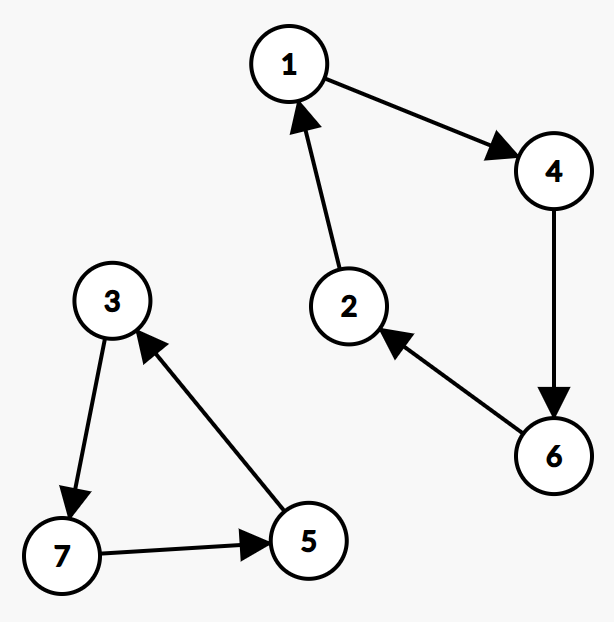
可以发现,这些结构就是置换环。置换环明确表达了一种交换关系。
例子:现在有一个序列$8,23,4,16,77,-5,53,100$,要从小到大排序,每次可以交换任意两个数字,最少需要交换几次?
我们可以把交换关系表示为置换环,比如,第一行我们表示下标,第二行原序列,第三行排序好的序列:
$$
\begin{pmatrix}
1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\
8&23&4&16&77&-5&53&100 \\
-5 & 4 & 8 & 16 & 23 & 53 & 77 & 100 \\
\end{pmatrix}
$$
可以发现,置换关系可以表示为:
$$
\begin{pmatrix}
1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\
3 & 5 & 2 & 4 & 7 & 1 & 6 & 8 \\
\end{pmatrix}
$$
也就是:
$$
(1,3,2,5,7,6)(4)(8)
$$
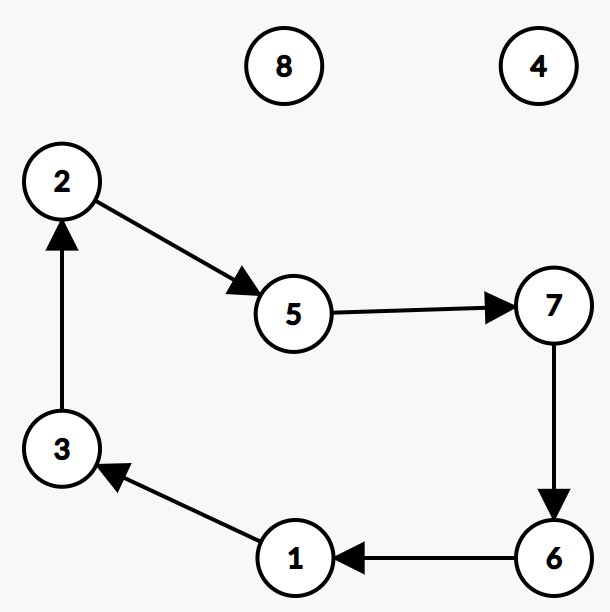
如果我们进行一次交换会怎样?例如,我们将原序列的下标$1$和下标$3$交换一下,那么:
$$
\begin{pmatrix}
1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\
4&23&8&16&77&-5&53&100 \\
-5 & 4 & 8 & 16 & 23 & 53 & 77 & 100 \\
\end{pmatrix}
$$
也就是置换关系变成:
$$
\begin{pmatrix}
1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\
2 & 5 & 3 & 4 & 7 & 1 & 6 & 8 \\
\end{pmatrix}
$$
也就是:
$$
(1,2,5,7,6)(3)(4)(8)
$$
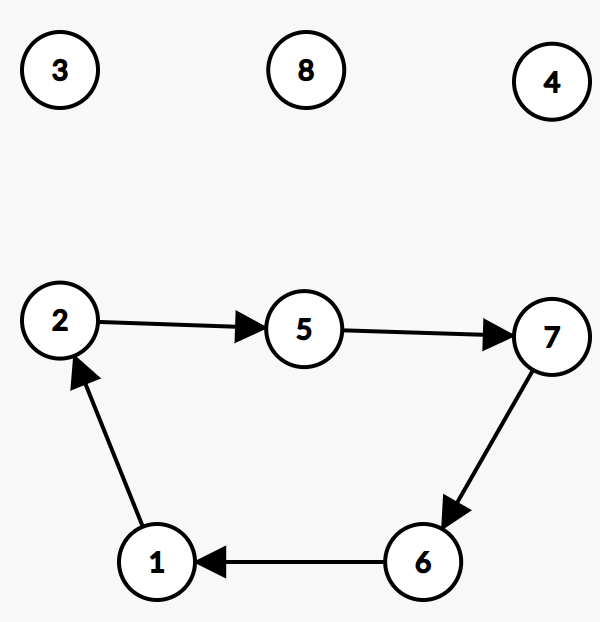
可以发现,进行一次交换,就会把置换环上的一个点从环中“摘除”出来,交换终点元素的前驱指向其后继,依旧构成一个环的形状。
所以,需要几次交换?$\sum (|环|-1)$
假设一共$k$个环,最小交换次数也可以表示为$n-k$。
根据上面的例子我们也能发现一个性质,也就是如果交换环上的两个点$u$和$v$,那么$u$继承$v$的后继,$v$继承$u$的后继。



发表评论