A CBC
按顺序输出字符串中的大写字母即可。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=1e5+5;
int T,n,m;
int main(){
string s;
cin>>s;
for(char c:s){
if(isupper(c)) cout<<c;
}
return 0;
}B Restaurant Queue
操作一入队，操作二出队，使用队列模拟即可
#include<bits/stdc++.h>
#define ll long long
using namespace std;
template<typename T>
void read(T &x) {x = 0;char ch = getchar();ll f = 1;while(!isdigit(ch)){if(ch == '-')f *= -1;ch = getchar();}while(isdigit(ch)){x = x * 10 + ch - 48; ch = getchar();}x *= f;}
template<typename T, typename... Args>
void read(T &first, Args& ... args) {read(first);read(args...);}
template<typename T>
void write(T arg) {T x = arg;if(x < 0) {putchar('-'); x =- x;}if(x > 9) {write(x / 10);}putchar(x % 10 + '0');}
template<typename T, typename ... Ts>
void write(T arg, Ts ... args) {write(arg);if(sizeof...(args) != 0) {putchar(' ');write(args ...);}}
const int N=1e5+5;
int T,n,m;
queue<int> q;
int main(){
read(n);
while(n--){
int opt,x;
read(opt);
if(opt==1){
read(x);
q.push(x);
}
else{
write(q.front()),putchar('\n');
q.pop();
}
}
return 0;
}C Dislike Foods
告诉我们每个食物需要用到的原材料，如果一个食物用到了讨厌的原材料，那么就不能食用。
一开始讨厌所有的原材料，然后$N$次输入，每次把一个讨厌的原材料转变成喜欢。请问，每次转变之后，能吃的食物种类有多少？
可以利用vector存一下每个原材料对应的食物编号，然后记录一下每个食物被讨厌的次数。如果一个食物的讨厌次数变成$0$，那么这个食物就能吃了。
参考代码：
#include<bits/stdc++.h>
#define ll long long
using namespace std;
template<typename T>
void read(T &x) {x = 0;char ch = getchar();ll f = 1;while(!isdigit(ch)){if(ch == '-')f *= -1;ch = getchar();}while(isdigit(ch)){x = x * 10 + ch - 48; ch = getchar();}x *= f;}
template<typename T, typename... Args>
void read(T &first, Args& ... args) {read(first);read(args...);}
template<typename T>
void write(T arg) {T x = arg;if(x < 0) {putchar('-'); x =- x;}if(x > 9) {write(x / 10);}putchar(x % 10 + '0');}
template<typename T, typename ... Ts>
void write(T arg, Ts ... args) {write(arg);if(sizeof...(args) != 0) {putchar(' ');write(args ...);}}
const int N=3e5+5;
int n,m,vis[N];
vector<int> dishes[N];
int main(){
read(n,m);
for(int i=1;i<=m;i++){
int k,x;
read(k);
while(k--){
read(x);
dishes[x].push_back(i);
vis[i]++;
}
}
int ans=0,B;
for(int i=1;i<=n;i++){
read(B);
for(int x:dishes[B]){
vis[x]--;
if(!vis[x]) ans++;
}
write(ans),putchar('\n');
}
return 0;
}D Line Crossing
问有多少条直线相交，我们可以用正难则反的原则，去考虑有多少条直线不相交，然后用总数减去不相交的直线数，就是相交的直线数。
总共有$M$条直线，所以总数为：
$$\frac{M(M-1)}{2}$$
现在问题转换为了：有多少对直线平行。因为只要不平行一定相交。
如果两个直线平行，假设第一条直线过的两个点是$(A_1,B_1)$，第二条直线过的两个点是$(A_2,B_2)$，可以想到点$A_1$和$A_2$的距离一定与$B_1$和$B_2$的距离相等。
也可以转换为，从$A_1$到$A_2$需要转几个点，那么从$B_2$到$B_1$也需要转几个点，两个方向相反，抵消掉了。所以能得到规律：
$$A_1+B_1 \bmod n=A_2+B_2\bmod n$$
至于为什么模$n$，因为$n$等分的圆，超过了$n$又从第一个点转回来了。
所以使用桶数组统计所有的$A+B$的数量，然后用总数减掉即可，记得开$long\ long$。
上面这个结论，多推几组样例，也能发现这个规律。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
template<typename T>
void read(T &x) {x = 0;char ch = getchar();ll f = 1;while(!isdigit(ch)){if(ch == '-')f *= -1;ch = getchar();}while(isdigit(ch)){x = x * 10 + ch - 48; ch = getchar();}x *= f;}
template<typename T, typename... Args>
void read(T &first, Args& ... args) {read(first);read(args...);}
template<typename T>
void write(T arg) {T x = arg;if(x < 0) {putchar('-'); x =- x;}if(x > 9) {write(x / 10);}putchar(x % 10 + '0');}
template<typename T, typename ... Ts>
void write(T arg, Ts ... args) {write(arg);if(sizeof...(args) != 0) {putchar(' ');write(args ...);}}
const int N=1e6+5;
int n,m,vis[N];
int main(){
read(n,m);
for(int i=1;i<=m;i++){
int a,b;
read(a,b);
vis[(a+b)%n]++;
}
ll ans=m*1ll*(m-1)>>1;
for(int i=0;i<n;i++){
ans-=vis[i]*1ll*(vis[i]-1)>>1;
}
write(ans);
return 0;
}E Payment Requeried
考虑状压DP
设$dp(i,j)$表示解决了$i$这个状态的题目，花费为$j$，所能获得的最大期望得分。其中$i$为状压。
可以想到，每次转移的时候，对于状态$dp(i,j)$，到底是选择哪个题目转移过来的呢？所以我们需要枚举求一个$max$。
注意，期望的公式为：
$$E=\sum_{i} P(i) \times V(i)$$
所以状态转移方程为：
$$dp(i,j)=max\{p[k]\times (dp(i\oplus (1<>k)\&1==1,j\geqslant c[k])$$
其中$k$是第$k$个物品。时间复杂度为$O(nm2^n)$
#include<bits/stdc++.h>
#define ll long long
using namespace std;
template<typename T>
void read(T &x) {x = 0;char ch = getchar();ll f = 1;while(!isdigit(ch)){if(ch == '-')f *= -1;ch = getchar();}while(isdigit(ch)){x = x * 10 + ch - 48; ch = getchar();}x *= f;}
template<typename T, typename... Args>
void read(T &first, Args& ... args) {read(first);read(args...);}
template<typename T>
void write(T arg) {T x = arg;if(x < 0) {putchar('-'); x =- x;}if(x > 9) {write(x / 10);}putchar(x % 10 + '0');}
template<typename T, typename ... Ts>
void write(T arg, Ts ... args) {write(arg);if(sizeof...(args) != 0) {putchar(' ');write(args ...);}}
const int N=1<<9;
int n,m,s[10],c[10];
double p[10];
double dp[N][5002];
int main(){
scanf("%d%d",&n,&m);
for(int i=0;i<n;i++){
int x;
scanf("%d%d%d",&s[i],&c[i],&x);
p[i]=x/100.0;
}
double ans=0;
for(int i=0;i<(1<<n);i++){
for(int j=0;j<=m;j++){
for(int k=0;k<n;k++){
if(j>=c[k]&&((i>>k)&1)){
double tmp=p[k]*(dp[i^(1<<k)][j-c[k]]+s[k])+(1-p[k])*dp[i][j-c[k]];
dp[i][j]=max(dp[i][j],tmp);
}
}
ans=max(ans,dp[i][j]);
}
}
printf("%lf",ans);
return 0;
}F Path to Interger
考虑折半查找。从起点搜一半，从终点搜一半，然后合并即可。
这里有一个细节，为了方便查找，我们两半搜索都搜索$n$步，让他们在中间相遇。所以需要注意，中间的点不要重复统计。可以选择在其中一个搜索中统计，另一个中不统计即可。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
template<typename T>
void read(T &x) {x = 0;char ch = getchar();ll f = 1;while(!isdigit(ch)){if(ch == '-')f *= -1;ch = getchar();}while(isdigit(ch)){x = x * 10 + ch - 48; ch = getchar();}x *= f;}
template<typename T, typename... Args>
void read(T &first, Args& ... args) {read(first);read(args...);}
template<typename T>
void write(T arg) {T x = arg;if(x < 0) {putchar('-'); x =- x;}if(x > 9) {write(x / 10);}putchar(x % 10 + '0');}
template<typename T, typename ... Ts>
void write(T arg, Ts ... args) {write(arg);if(sizeof...(args) != 0) {putchar(' ');write(args ...);}}
const int N=25;
int dx[]={1,0,-1,0};
int dy[]={0,1,0,-1};
int n,m,a[N][N];
ll ans,p10[N<<1];
vector<int> v[N][N];
void dfs1(int x,int y,int step,ll val){
if(step==n){
v[x][y].push_back((val*10%m+a[x][y])%m*p10[n-1]%m);
return ;
}
for(int i=0;i<=1;i++){
int tx=x+dx[i],ty=y+dy[i];
if(tx>=1&&ty>=1&&tx<=n&&ty<=n){
dfs1(tx,ty,step+1,(val*10%m+a[x][y])%m);
}
}
}
void dfs2(int x,int y,int step,ll val){
if(step==n){
int idx=upper_bound(v[x][y].begin(),v[x][y].end(),m-val-1)-v[x][y].begin()-1;
if(idx>=0) ans=max(ans,(val+v[x][y][idx])%m);
idx++;
if(idx<v[x][y].size()) ans=max(ans,(val+v[x][y][idx])%m);
return ;
}
for(int i=2;i<=3;i++){
int tx=x+dx[i],ty=y+dy[i];
if(tx>=1&&ty>=1&&tx<=n&&ty<=n){
dfs2(tx,ty,step+1,(val+a[x][y]*p10[step-1]%m)%m);
}
}
}
int main(){
read(n,m);
p10[0]=1;
for(int i=1;i<=(n<<1);i++) p10[i]=p10[i-1]*10%m;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
read(a[i][j]);
}
}
dfs1(1,1,1,0);
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(v[i][j].size()){
sort(v[i][j].begin(),v[i][j].end());
}
}
}
dfs2(n,n,1,0);
write(ans);
return 0;
}可以发现，二分之后还有一个比较的过程。
我们想的最理想的情况是找到一个小于等于$m-val-1$最大的数字和$val$相加，这样就能尽量的大。
但是理想情况不存在呢？也就是说到了$(x,y)$这个位置，小于等于$m-val-1$的数字都不存在，所以只能向后找了。
G Sum of Prod of Mod of Linear
前置知识：类欧几里得算法
根据学过的类欧几里得算法的知识，我们知道如下几个公式：
$$F(a,b,c,n)=\sum_{i=0}^n \lfloor \frac{ai+b}{c} \rfloor \\ G(a,b,c,n)=\sum_{i=0}^n i \lfloor \frac{ai+b}{c} \rfloor \\ H(a,b,c,n)=\sum_{i=0}^n \lfloor \frac{ai+b}{c} \rfloor^2$$
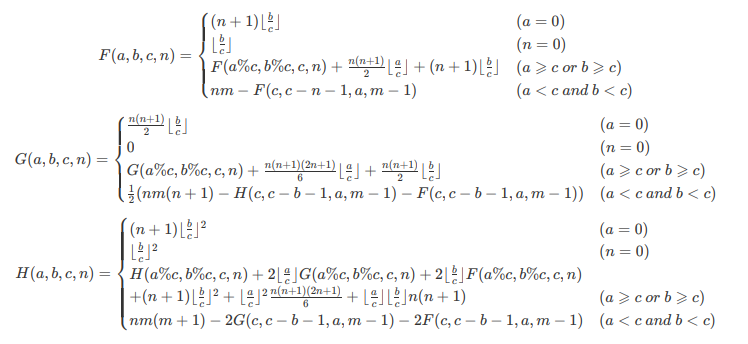
根据这几个公式来求解这个题。
看到这个题的题意：给定$N,M,A,B_1,B_2$，并且$0\leqslant A,B_1,B_2 < M$，求：
$$\sum_{i=0}^{N-1}\{(Ai+B_1)\bmod M\}\{(Ai+B_2)\bmod M\}$$
我们知道：$a\% b=a-\lfloor \frac{a}{b}\rfloor b$，所以有：
$$\begin{aligned}
&\sum_{i=0}^{N-1}\{(Ai+B_1)\bmod M\}\{(Ai+B_2)\bmod M\}\\
&=\sum_{i=0}^{N-1}\{ (Ai+B_1)-\lfloor \frac{Ai+B_1}{M}\rfloor M \}\{ (Ai+B_2)-\lfloor \frac{Ai+B_2}{M}\rfloor M \}\\
&= \sum_{i=0}^{N-1}((Ai+B_1)(Ai+B_2)-(Ai+B_1)M\lfloor \frac{Ai+B_2}{M}\rfloor-(Ai+B_2)M\lfloor \frac{Ai+B_1}{M}\rfloor+M^2\lfloor\frac{Ai+B_1}{M}\rfloor \lfloor\frac{Ai+B_2}{M}\rfloor)
\end{aligned}$$
做一下简单的拆分和整理，得到：
$$\begin{aligned}
&=A\sum_{i=0}^{N-1} i^2 +A(B_1+B_2)\sum_{i=0}^{N-1}i+\sum_{i=0}^{N-1}B_1B_2\\
&-M(A\sum_{i=0}^{N-1}i\lfloor\frac{Ai+B_1}{M}\rfloor+A\sum_{i=0}^{N-1}i\lfloor\frac{Ai+B_2}{M}\rfloor+B_1\sum_{i=0}^{N-1}\lfloor \frac{Ai+B_2}{M}\rfloor)+B_2\sum_{i=0}^{N-1}\lfloor \frac{Ai+B_1}{M}\rfloor)\\
& +M^2\sum_{i=0}^{N-1}\lfloor \frac{Ai+B_1}{M}\rfloor \lfloor \frac{Ai+B_2}{M}\rfloor
\end{aligned}$$
换成之前三种函数的形式，并将其中一些能直接计算出来的式子计算出来：
$$\begin{aligned}
&=\frac 16 A^2N(N-1)(2N-1)+\frac 12 AN(N-1)(B_1+B_2)+NB_1B_2\\
&-M(A(G(A,B_1,M,N-1)+G(A,B_2,M,N-1))+B_1F(A,B_2,M,N-1)+B_2F(A,B_1,M,N-1))\\
&+M^2\sum_{i=0}^{N-1}\lfloor \frac{Ai+B_1}{M}\rfloor \lfloor \frac{Ai+B_2}{M}\rfloor
\end{aligned}$$
观察整个式子，可以发现，其他部分我们都已经解决了，只有一个部分需要解决：
$$\sum_{i=0}^{N-1}\lfloor \frac{Ai+B_1}{M}\rfloor \lfloor \frac{Ai+B_2}{M}\rfloor $$
观察数据范围：$0\leqslant B_1,B_2 < M$，其实$B_1$和$B_2$可以互换，所以我们假设$B_2\geqslant B_1$。
所以，显然可以发现，$\lfloor\frac{Ai+B_1}{M}\rfloor$和$\lfloor \frac{Ai+B_2}{M}\rfloor$相比，要么相等，要么差$1$，所以我们可以转换成计算差值。
首先，可以有：
$$\begin{aligned}
&\sum_{i=0}^{N-1}\lfloor\frac{Ai+B_1}{M}\rfloor \lfloor\frac{Ai+B_2}{M}\rfloor -\sum_{i=0}^{N-1}\lfloor\frac{Ai+B_2}{M}\rfloor^2\\
&=-\sum_{i=0}^{N-1}\lfloor\frac{Ai+B_2}{M}\rfloor(\lfloor \frac{Ai+B_2}{M}\rfloor-\lfloor \frac{Ai+B_1}{M}\rfloor)
\end{aligned}$$
之前说$0\leqslant B_1\leqslant B_2 < M$，所以上面式子的括号里的值要么是$0$，要么是$1$。
考虑对于一个固定的值$c=\lfloor \frac{Ai+B_2}{M} \rfloor$，我们将这个式子等于$c$的值对应的$i$的最小值写作$d_{2,c}$，$B_1$对应的式子的$i$的最小值就是$d_{1,c}$。
可以知道$d_{2,c}\leqslant i < d_{2,c+1}$。
考虑$d_{i,c}$的值。考虑做如下的转换：
$$c=\lfloor \frac{Ai+B_2}{M}\rfloor
\\c\leqslant \frac{Ai+B_2}{M}$$
为何？如果$M|A_i+B_2$，那么就是相等，否则就是小于，所以得到了上面这个不等式。做不等式的简单变换，得到：
$$i\geqslant \frac{cM-B_2}{A}$$
由于$i$始终是整数，所以得到：
$$i_{min}=\lceil\frac{cM-B_2}{A}\rceil$$
向上取整的式子我们不好处理，但是我们知道：
$$\lceil\frac{a}{b}\rceil=\lfloor\frac{a+b-1}{b}\rfloor$$
上面的$i_{min}$其实就是$d_{2,c}$，所以得到：
$$d_{2,c}=min(N,\lfloor\frac{cM+A-B_2-1}{A}\rfloor)$$
$d_{1,c}$同理。
既然$B_2$对应的式子为$c$，那么在这个范围内，$B_1$对应的式子的值为$c-1$才会对答案有贡献。也就是$d_{2,c}\leqslant i < d_{1,c}$。
从这个角度出发，重新整理式子。设$X=\lfloor\frac{A(N-1)+B_2}{M}\rfloor$，也就是$c_{max}$，我们整理成枚举$c$的值进行计算：
$$\begin{aligned}
&-\sum_{i=0}^{N-1}\lfloor\frac{Ai+B_2}{M}\rfloor(\lfloor \frac{Ai+B_2}{M}\rfloor-\lfloor \frac{Ai+B_1}{M}\rfloor)\\
&=-\sum_{c=0}^{X}c\sum_{k=d_{2,c}}^{d_{1,c}-1}1\\
&=-\sum_{c=0}^{X}c(d_{1,c}-d_{2,c})\\
&=-\sum_{c=0}^{X-1}c(d_{1,c}-d_{2,c})-X(d_{1,X}-d_{2,X})
\end{aligned}$$
对于$c < X$，我们有$d_{k,c}=\lfloor\frac{cM+A-B_i-1}{A}\rfloor$，这部分我们也可以用类欧来解决了：
$$\begin{aligned}
&-\sum_{c=0}^{X-1}c(d_{1,c}-d_{2,c})\\
&=-\sum_{c=0}^{X-1}c(\lfloor \frac{cM+A-B_1 -1}{A}\rfloor-\lfloor \frac{cM+A-B_2 -1}{A}\rfloor)\\
&=\sum_{c=0}^{X-1}c\lfloor \frac{cM+A-B_2 -1}{A}\rfloor-\sum_{c=0}^{X-1}c\lfloor \frac{cM+A-B_1 -1}{A}\rfloor
\end{aligned}$$
给变量$c$换个名字是不是会更眼熟？
$$\begin{aligned}
&\sum_{i=0}^{X-1}i\lfloor \frac{Mi+A-B_2 -1}{A}\rfloor-\sum_{i=0}^{X-1}i\lfloor \frac{Mi+A-B_1 -1}{A}\rfloor\\
&=G(M,A-B_2 -1,A,X-1)-G(M,A-B_1 -1,A,X-1)
\end{aligned}$$
注意，这部分是用来算差值的，也就是说：
$$\begin{aligned}
&\sum_{i=0}^{N-1}\lfloor \frac{Ai+B_1}{M}\rfloor \lfloor \frac{Ai+B_2}{M}\rfloor\\
&=\sum_{i=0}^{N-1}\lfloor\frac{Ai+B_2}{M}\rfloor^2+(\sum_{i=0}^{N-1}\lfloor\frac{Ai+B_1}{M}\rfloor \lfloor\frac{Ai+B_2}{M}\rfloor -\sum_{i=0}^{N-1}\lfloor\frac{Ai+B_2}{M}\rfloor^2)\\
&=H(A,B_2,M,N-1)+G(M,A-B_2 -1,A,X-1)-G(M,A-B_1 -1,A,X-1)-X(d_{1,X}-d_{2,X})
\end{aligned}$$
如此，我们就把所有的问题，都化归到了$F,G,H$这三个函数的求解问题上了。总结一下：
$$\begin{aligned}
&\sum_{i=0}^{N-1}\{(Ai+B_1)\bmod M\}\{(Ai+B_2)\bmod M\}\\
&=\frac 16 A^2N(N-1)(2N-1)+\frac 12 AN(N-1)(B_1+B_2)+NB_1B_2\\
&-M(A(G(A,B_1,M,N-1)+G(A,B_2,M,N-1))+B_1F(A,B_2,M,N-1)+B_2F(A,B_1,M,N-1))\\
&+M^2(H(A,B_2,M,N-1)+G(M,A-B_2 -1,A,X-1)-G(M,A-B_1 -1,A,X-1)-X(d_{1,X}-d_{2,X}))
\end{aligned}$$
注意，类欧求解的时候别忘了依旧是共同递归，这样能保证时间复杂度在$log$级别。同时，这个题的数据很大，所以使用了__int128
参考代码：
#include<bits/stdc++.h>
#define ll __int128
using namespace std;
template<typename T>
void read(T &x) {x = 0;char ch = getchar();ll f = 1;while(!isdigit(ch)){if(ch == '-')f *= -1;ch = getchar();}while(isdigit(ch)){x = x * 10 + ch - 48; ch = getchar();}x *= f;}
template<typename T, typename... Args>
void read(T &first, Args& ... args) {read(first);read(args...);}
template<typename T>
void write(T arg) {T x = arg;if(x < 0) {putchar('-'); x =- x;}if(x > 9) {write(x / 10);}putchar(x % 10 + '0');}
template<typename T, typename ... Ts>
void write(T arg, Ts ... args) {write(arg);if(sizeof...(args) != 0) {putchar(' ');write(args ...);}}
struct node{
ll f,g,h;
};
node getans(ll a,ll b,ll c,ll n){
node ans;
if(!a){
ans.f=(b/c)*(n+1);
ans.g=(b/c)*n*(n+1)/2;
ans.h=(b/c)*(b/c)*(n+1);
}
else if(!n){
ans.f=b/c;
ans.g=0;
ans.h=(b/c)*(b/c);
}
else if(a>=c||b>=c){
node tmp=getans(a%c,b%c,c,n);
ans.f=((tmp.f
+n*(n+1)/2*(a/c))
+(b/c)*(n+1));
ans.g=((tmp.g
+n*(n+1)*(2*n+1)/6*(a/c))
+n*(n+1)/2*(b/c));
ans.h=(((((tmp.h
+2*(a/c)*tmp.g)
+2*(b/c)*tmp.f)
+(n+1)*(b/c)*(b/c))
+(a/c)*(a/c)*n*(n+1)*(2*n+1)/6)
+(a/c)*(b/c)*n*(n+1));
}
else{
ll m=(a*n+b)/c;
node tmp=getans(c,c-b-1,a,m-1);
ans.f=(n*m-tmp.f);
ans.g=(m*n*(n+1)
-tmp.h
-tmp.f)/2;
ans.h=(((n*m*(m+1)
+(-2*tmp.g))
+(-2*tmp.f))
+(-ans.f));
}
return ans;
}
ll T,n,m,a,b1,b2;
int main(){
read(T);
while(T--){
read(n,m,a,b1,b2);
if(b1>b2) swap(b1,b2);
if(!a){
write(n*1ll*b1*b2),putchar('\n');
continue;
}
ll ans=n*(n-1)*(2*n-1)/6*a*a+n*(n-1)/2*a*(b1+b2);
ans+=n*b1*b2;
node func1=getans(a,b1,m,n-1),func2=getans(a,b2,m,n-1);
ans+=-m*(a*(func1.g+func2.g)+b1*func2.f+b2*func1.f);
ll X=(a*(n-1)+b2)/m;int t=1;
while(t*a-b2-1<0) t++;
ll sum=func2.h+getans(m,t*a-b2-1,a,X-1).g-getans(m,t*a-b1-1,a,X-1).g;
sum-=X*(min((ll)(n),(X*m+a-b1-1)/a)-min((ll)(n),(X*m+a-b2-1)/a));
ans+=m*m*sum;
write(ans),putchar('\n');
}
return 0;
}
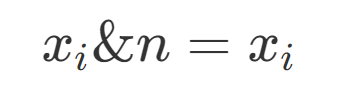
发表评论