中国剩余定理(CRT)
中国剩余定理(孙子定理,Chinese Remainder Theorem,缩写为CRT)用来解同余方程组,形式如下:
其中$r_1,r_2,\cdots,r_n$两两互质。这个方程组一定是有解的。
算法流程:
- 计算所有模数的乘积$LCM = r_1r_2\cdots r_n$。
- 计算$m_i = \frac{LCM}{r_i}$,并求出$m_i$在模$r_i$下的逆元$m_i^{-1}$。
- 计算$c_i = m_im_i^{-1}$。
- 计算最终答案$x = \sum_{i=1}^n a_i c_i(\mod{LCM})$。
CRT的证明
这是一个构造问题。我们构造一个$c$序列:
可知:
上面的模$LCM$也可以看作是加上$k$个$LCM$,$k$是任意整数。思考上面这个式子,可以知道,对于每个同余方程,$x$的值都满足这个方程。所以这种构造是合理的。
那么问题的关键就转换成了如何构造$c$序列。考虑构造一个$m$序列:
这样,我们知道:
$$\forall 1\leq i,j\leq n,i\neq j ,st. m_i\equiv 0(\mod r_j)$$
那么,对于每个$m_i$,我们只需要求出它在模$r_i$下的逆元$m_i^{-1}$即可。下面式子中的$m_i^{-1}$都是模$r_i$意义下的逆元。
这样:
$$\forall 1\leq i,j\leq n,i\neq j ,st.\ m_i m_i^{-1}\equiv 0(\mod r_j) \ m_i m_i^{-1}\equiv 1(\mod{r_i})$$
所以,$c_i=m_i m_i^{-1}$,就完美满足了我们上面的所有条件。
CRT的代码实现
ll CRT(ll k,ll* a,ll* r){
ll LCM=1,ans=0;
for(int i=1;i<=k;i++) LCM*=r[i];
for(int i=1;i<=k;i++){
ll m=LCM/r[i],x,y;
exgcd(m,r[i],x,y);
x=(x%r[i]+r[i]-1)%r[i]+1;
ans=(ans+a[i]*m%LCM*x%LCM)%LCM;
}
return (ans%LCM+LCM)%LCM;
}要注意,如果数据过于极限,计算$ans$时的乘法可能会爆$\text{long long}$,所以需要使用龟速乘或者使用$\text{long double}$自然溢出。不论怎么实现的,函数$Mul(a,b,mod)$的功能是计算$a\times b(\mod{mod})$。
ll Mul(ll a,ll b,ll mod){//long double自然溢出
ll tmp=a*b-(ll)((long double)a*b/mod+0.1)*mod;
return tmp<0?tmp+mod:tmp;
}
ll CRT(ll k,ll* a,ll* r){
ll LCM=1,ans=0;
for(int i=1;i<=k;i++) LCM*=r[i];
for(int i=1;i<=k;i++){
ll m=LCM/r[i],x,y;
exgcd(m,r[i],x,y);
x=(x%r[i]+r[i]-1)%r[i]+1;
ans=(ans+Mul(Mul(a[i],m,LCM),x,LCM))%LCM;
}
return (ans%LCM+LCM)%LCM;
}扩展中国剩余定理(EXCRT)
相对于中国剩余定理,扩展中国剩余定理($\text{Extended Chinese Remainder Theorem}$,缩写为$\text{EXCRT}$)可以解决模数不互质的情况。形式如下:
其中$r_1,r_2,\cdots,r_n$不要求两两互质。这个方程组不一定有解。
算法流程:
目的是每次把第$i$个方程合并到第$1$个方程上。
$\text{for}$循环从$2$到$n$:
1、定义$r_1,r_2,k_1,k_2,c=a_i - a_1$
2、$\text{exgcd}$获得关于$r_1k_1+r_ik_2=gcd(r_1,r_i)$的一组解,同时得到$d=gcd(r_1,r_2)$
3、如果无解,返回$-1$
4、计算出新的$k_1$的值:$k_1=k_1 \cdot \frac{c}{d}(\mod{\frac{r_i}{d}})$
5、更新$a_1+=k_1r_1,r_1*=\frac{r_i}{d}$
最后$a_1$的值就是最终的解。
EXCRT的证明
首先考虑两个方程的情况:
上面的方程组可以转化为:
其中$k_1,k_2$为任意整数。那么,我们可以得到:
整理一下得到:
由于$k_1,k_2$都是未知数,所以也可以写作:
这个式子,我们可以通过$\text{exgcd}$解这个方程,得到$k_1,k_2$的一个解。当然,如果$a_2-a_1$不能被$gcd(r_1,r_2)$整除,那么这个方程无解。换句话说,整个方程组也无解。
设$d=gcd(r_1,r_2)$,那么上面的方程转化为:
可知$gcd(\frac{r_1}{d},\frac{r_2}{d})=1$,所以我们$exgcd$求解的必然是方程$\frac{r_1}{d}k_1+\frac{r_2}{d}k_2=1$的一个解。所以,我们最后的解还要乘以$\frac{a_2-a_1}{d}$。
那么,我们得到这两个变量的解有什么用呢?根据我们之前学过的扩欧的知识,我们知道:
带入到一开始的式子中:
换成同余形式,也就是:
这样,原本的:
就转化为了:
也就是说,两个同余方程融合成了一个。新的方程中,新的$a_1$的值是原来的$a_1 +k_1 r_1$,新的$r_1$的值是原来的$lcm(r_1,r_2)$也就是$r_1\times \frac{r_2}{gcd(r_1,r_2)}$。那么以此类推,我们就可以将$n$个同余方程融合成一个。这样就得到了方程组的解。
EXCRT的代码实现
ll EXCRT(ll k,ll* a,ll* r){
ll a1=a[1],r1=r[1];
for(int i=2;i<=k;i++){
ll k1,k2,c=((a[i]-a1)%r[i]+r[i])%r[i];
ll d=exgcd(r1,r[i],k1,k2);
if(c%d) return -1;
k1=Mul(k1,c/d,r[i]/d);
a1+=k1*r1;
r1*=r[i]/d;
a1=(a1%r1+r1)%r1;
}
return (a1%r1+r1)%r1;
}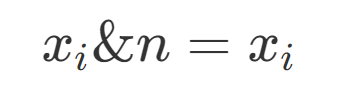
发表评论